The Systemic Risk Analysis presents a variety of risk measures for major Global Financial Firms. These measures are updated weekly and reveal several dimensions of risk. Historical estimates of each of these risk measures can be plotted to see the changing performance of individual firms.

A financial firm will be unable to function when the value of its equity falls to a sufficiently small fraction of its outstanding liabilities. In good times, such a firm will likely be acquired, may be able to raise new capital or may face an orderly bankruptcy. If this capital shortage occurs at a time when the financial sector is already financially constrained, then the government faces the question of whether to rescue the firm with taxpayer money as other avenues are no longer available. In the theoretical analysis of Acharya, Pederson, Phillipon and Richardson (2010), such a capital shortage is damaging to the real economy as the failure of this firm will have repercussions throughout the financial and real sectors. Consequently a firm is systemically risky if it is likely to face a capital shortage just when the financial sector itself is weak.

The analysis presented here seeks to measure these concepts for major Global Financial Firms. The program calculates the expected capital shortage faced by a firm in a potential future financial crisis. Conceptually this calculation is like the stress tests that are regularly applied to financial firms, however here it is done with only publicly available information and is quick and inexpensive to compute.

Asynchronous Prices and Dynamic Conditional Beta

In a global model, data are recorded as closing prices on a specific date but these closing prices are not necessarily at the same time. We can think of New York as the last market to close on a given day and Asia to be the first to close. European markets are between. As a consequence, the New York data has information that is not yet included in the other asset prices so there is predictability from New York to other markets. This predictability lasts only one day by efficient market arguments.

Consider two stock prices and corresponding returns, $r_i$ and $r_m$. These are close to close returns on a financial firm in a market different from New York and a broad market return recorded at the New York close. Because $r_{\mathrm{i,t}}$ overlaps both $r_{\mathrm{m,t}}$ and $r_{\mathrm{m,t-1}}$ we need the joint distribution of these three returns. In the figure, the blue segment overlaps both red and yellow.

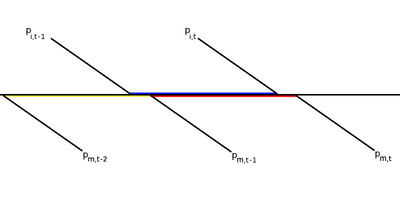
Conceptually the joint conditional distribution of the three returns can be expressed conditional on information before any was observed. Only at $t-2$ will this be satisfied. Clearly $r_{\mathrm{i,t-1}}$ will have information about $r_{\mathrm{m,t-1}}$ so it cannot be conditioned upon. Adding the assumption of normality$$\begin{array}{}\text{(1)}& \left(\begin{array}{c}{r}_{\mathrm{i,t}}\\ r_{\mathrm{m,t}}\\ r_{\mathrm{m,t-1}}\end{array}\right)|F_{\mathrm{t-2}}~N\left(0,H_t\right)\end{array}$$The conditional distribution of the first of these variables given the second and third will then be linear and normal. It can be written as:$$\begin{array}{}\text{(2)}& R_{\mathrm{i,t}}={\beta }_{\mathrm{i,t}}{R}_{\mathrm{m,t}}+{\gamma }_{\mathrm{i,t}}{R}_{\mathrm{m,t-1}}+{\mu }_{\mathrm{i,t}}\end{array}$$Where the coefficients are given by the inverse of the covariance matrix of the two regressors times the covariances of each with the dependent variable. In the notation of $\mathrm{(2)}$, this is$$\begin{array}{}\text{(3)}& \left(\begin{array}{}{\beta }_{\mathrm{i,t}}\\ {\gamma }_{\mathrm{i,t}}\end{array}\right)& =& {\left(\begin{array}{}{H}_{r_{\mathrm{m,t}},r_{\mathrm{m,t}}}{H}_{r_{\mathrm{m,t}},r_{\mathrm{m,t-1}}}\\ H_{r_{\mathrm{m,t}},r_{\mathrm{m,t-1}}}{H}_{r_{\mathrm{m,t-1}},r_{\mathrm{m,t-1}}}\\ \end{array}\right)}^{-1}& \left(\begin{array}{}{H}_{r_{\mathrm{m,t}},r_{\mathrm{i,t}}}\\ H_{r_{\mathrm{m,t-1}},r_{\mathrm{i,t}}}\end{array}\right)\end{array}$$This is the insight of the DCB model. Assuming that $r_m$ is dynamically uncorrelated, then the regressor matrix is diagonal, and the coefficients are simply univariate dynamic regression coefficients given as $$\begin{array}{}\text{(4)}& {\beta }_{\mathrm{i,t}}=\frac{E\left(r_{\mathrm{i,t}}{r}_{\mathrm{m,t}}|F_{\mathrm{t-2}}\right)}{E\left(r_{\mathrm{m,t}}^2|F_{\mathrm{t-2}}\right)},{\gamma }_{\mathrm{i,t}}=\frac{E\left(r_{\mathrm{i,t}}{r}_{\mathrm{m,t-1}}|F_{\mathrm{t-2}}\right)}{E\left(r_{\mathrm{m,t-1}}^2|F_{\mathrm{t-2}}\right)}\end{array}$$This specification can be written as$$\begin{array}{}\text{(5)}& \begin{array}{c}{r}_{\mathrm{m,t}}|F_{\mathrm{t-1}}~N\left(0,h_{\mathrm{m,t}}\right)\text{, or}\hfill \\ r_{\mathrm{m,t}}=\sqrt{h_{\mathrm{m,t}}}{\epsilon }_{\mathrm{m,t}}\hfill \end{array}\end{array}$$Although prices are measured asynchronously, each asset price should be a Martingale with respect to its own information set and have non-autocorrelated returns. The autocorrelation of $r_i$ can now be calculated from$$\begin{array}{}\text{(6)}& \begin{array}{ccc}\hfill E\left(r_{\mathrm{i,t}}{r}_{\mathrm{i,t-1}}\right)& \hfill =\hfill & E\left({\beta }_{\mathrm{i,t}}{r}_{\mathrm{m,t}}+{\gamma }_{\mathrm{i,t}}{r}_{\mathrm{m,t-1}}+{\mu }_t\right)\left({\beta }_{\mathrm{i,t-1}}{r}_{\mathrm{m,t-1}}+{\gamma }_{\mathrm{i,t-1}}{r}_{\mathrm{m,t-2}}+{\mu }_{\mathrm{t-1}}\right)\hfill \\ & \hfill =\hfill & E\left({\gamma }_{\mathrm{i,t}}{\beta }_{\mathrm{i,t-1}}{r}_{\mathrm{m,t-1}}^2\right)+E\left({\mu }_t{\mu }_{\mathrm{t-1}}\right)\hfill \end{array}\end{array}$$This can only be zero if there is no asynchronicity of prices so that either $\beta$ or $\gamma$ is zero, or if $\mu$ has an offsetting autocorrelation which is required to be negative. The same computation for two lags immediately shows that there is no second order autocorrelation so this can be only an $\mathrm{MA}\left(1\right)$.

A second implication is that $\mathrm{MES}$ should be defined in terms of expectations with a two day lag. In the case of non-synchronous returns it is natural to define $\mathrm{MES}$ as the expected loss over the next two days if the market today is less than $c$. This should be evaluated using the most recent available information but there is a logical flaw if we include yesterday in the information set.$$\begin{array}{}\text{(7)}& \begin{array}{ccc}\hfill \mathrm{MES}& \hfill =\hfill & {\mathrm{-E}}_{\mathrm{t-2}}\left(r_{\mathrm{i,t+1}}+r_{\mathrm{i,t}}|r_{\mathrm{m,t}}<c\right)\hfill \\ & \hfill =\hfill & {\mathrm{-E}}_{\mathrm{t-2}}\left({\beta }_{\mathrm{i,t+1}}{r}_{\mathrm{m,t+1}}+{\gamma }_{\mathrm{i,t+1}}{r}_{\mathrm{m,t}}+{\beta }_{\mathrm{i,t}}{r}_{\mathrm{m,t}}+{\gamma }_{\mathrm{i,t}}{r}_{\mathrm{m,t-1}}|r_{\mathrm{m,t}}<c\right)\hfill \\ & \hfill =\hfill & {\mathrm{-E}}_{\mathrm{t-2}}\left(\left({\gamma }_{\mathrm{i,t+1}}+{\beta }_{\mathrm{i,t}}\right)E_{\mathrm{t-2}}\left(r_{\mathrm{m,t}}|r_{\mathrm{m,t}}<c\right)\right)\hfill \\ & \hfill =\hfill & -\left({\gamma }_{\mathrm{i,t+1}}+{\beta }_{\mathrm{i,t}}\right)E_{\mathrm{t-1}}\left(r_{\mathrm{m,t}}|r_{\mathrm{m,t}}<c\right)\hfill \end{array}\end{array}$$This uses the law of iterated expectations and the assumption that the expectation of $r_{\mathrm{m,t+1}}$ and $r_{\mathrm{m,t-1}}$ are both zero given that $r_{\mathrm{m,t}}<c$. It also in the last step approximates $\gamma$ and the market ES as almost a martingale so that the two step forecast and the one step forecast are similar.

We propose a generalization of equation (2) which nests the time varying beta model and the constant beta model allowing the data to pick which is a better model. Thus the regression equation would be written with four regression parameters as$$\begin{array}{}\text{(8)}& r_{\mathrm{i,t}}=\left({\Phi }_1+{\Phi }_2{\beta }_{\mathrm{i,t}}\right)r_{\mathrm{m,t}}+\left({\Phi }_3+{\Phi }_4{\gamma }_{\mathrm{i,t}}\right)r_{\mathrm{m,t-1}}+{\mu }_t\end{array}$$Thus the estimated beta has a fixed component and a time varying component. This specification can reduce the noise if the covariances are badly estimated and appears to work well in our data. The regression should be estimated by assuming that $\mu$ is heteroskedastic and $\mathrm{MA}\left(1\right)$. Thus the equation becomes$$\begin{array}{}\text{(9)}& r_{\mathrm{i,t}}=\left({\Phi }_1+{\Phi }_2{\beta }_{\mathrm{i,t}}\right)r_{\mathrm{m,t}}+\left({\Phi }_3+{\Phi }_4{\gamma }_{\mathrm{i,t}}\right)r_{\mathrm{m,t-1}}+\sqrt{h_{\mathrm{i,t}}}{\xi }_{\mathrm{i,t}}+{\Phi }_5\sqrt{h_{\mathrm{i,t-1}}}{\xi }_{\mathrm{i,t-1}}\end{array}$$

Systemic Risk Analysis

This calculation takes two steps. First it estimates the expected fractional loss of the firm equity in a crisis when the aggregate market declines significantly in a six-month period. This is called Long-Run Marginal Expected Shortfall or LRMES. Specifically, it is calculated as 1-exp(log(1-d)*beta), where dis the six-month crisis threshold for the market index decline and its default value is 40%, and beta is the firm's beta coefficient. By default, the crisis threshold for market decline is set to be 40%, consistent with Systemic Risk Analyses with and without Simulation for U.S. Financials. Secondly, equity losses expected in a crisis are combined with current equity market value and outstanding measures of debt to determine how much capital would be needed in such a crisis. By default, the prudential capital requirement used in calculating such capital shortfalls is set to be 8% for firms in Africa, Asia and Americas and 5.5% for firms in Europe due to differences in accounting standards.

Systemic Risk (SRISK)

SRISK is the expected capital shortfall of this firm if there is another crisis. The NYU Stern Systemic Risk Ranking, SRISK%, is the firm’s percentage of financial sector capital shortfall. Firms with a high percentage of capital shortfall in a crisis are not only the biggest losers in a crisis but also are the biggest contributors to the crisis.

Capital shortfall ($\mathrm{SRISK}$) is computed as$$\begin{array}{}\text{(10)}& \mathrm{SRISK}=k\cdot \mathrm{DEBT}-\left(1-k\right)\cdot \mathrm{EQUITY}\cdot \left(1-\mathrm{LRMES}\right)\end{array}$$where $k$ is the capital requirement, $\mathrm{LRMES}$ is the Long-Run Marginal Expected Shortfall, $\mathrm{EQUITY}$is the current market capitalization of this firm and $\mathrm{DEBT}$ is the book value of debt which is calculated as the book value of assets minus the book value of equity.

To sort the firms by any of these categories, simply click on the heading. To plot any of the series, click on the firm name and select the series to be plotted. You can select the time horizon of the plot. To see help, click on the & quot;?s" in the page.

Separate Accounts

Some of the firms in our Systemic Risk Analysis, primarily life insurers, have an item on their balance sheets known as Separate Accounts. In these companies, premiums are accumulated in investment funds such as variable annuities. These can be withdrawn, often with penalties, and have payouts at guaranteed levels. They are recorded as both assets and liabilities on the balance sheet. An estimate of the value of the guarantees is also recorded as a liability. Including separate accounts as assets which require capital may overstate the need for capital. However, ignoring them will understate the need for precautionary capital.

For insurance companies in calm times, when 40% of separate accounts are included in total liabilities, capital ratios are typically about 8%. This is consistent with our default capital requirement. Hence, we reduce $\mathrm{DEBT}$ so that only 40% of liabilities due to separate accounts are included by default.

To change the percentage of separate accounts that is included, enter a new value into the spinner in the Options sidebar.

Systemic Risk Decomposition

On the V-Lab Systemic Risk Pages, you can see estimates of the amount of capital that firms will need in the event of a crisis, SRISK, and you can view the components and changes in SRISK over time. But what causes SRISK to change? If we look at the SRISK equation, we can get a better idea of the underlying aspects behind these changes. From equation (1) we can see that the total differential of $\mathrm{SRISK}$ is given by:$$\begin{array}{}\text{(11)}& \Delta \mathrm{SRISK}=k\cdot d\mathrm{DEBT}-\left(1-k\right)\cdot \left(1-\mathrm{LRMES}\right)\cdot d\mathrm{EQUITY}+\left(1-k\right)\cdot \mathrm{EQUITY}\cdot d\mathrm{LRMES}\end{array}$$Thus, the change in SRISK for any given firm ($\Delta \mathrm{SRISK}$) can be decomposed into three parts:

• $\Delta \left(\mathrm{DEBT}\right)=k\cdot d\mathrm{DEBT}$ — This is the contribution to SRISK of the firm's debt. As a firm takes on more debt, the contribution to SRISK will be positive. Since this data is reported no more frequently than on a quarterly basis, month-to-month values can show no change in $\Delta \left(\mathrm{DEBT}\right)$.
• $\Delta \left(\mathrm{EQUITY}\right)=-\left(1-k\right)\cdot \left(1-\mathrm{LRMES}\right)\cdot d\mathrm{EQUITY}$ — This measure shows how changes in a firm's equity position affects SRISK. A decline in the market capitalization of a company will increase SRISK.
• $\Delta \left(\mathrm{RISK}\right)=\left(1-k\right)\cdot \mathrm{EQUITY}\cdot d\mathrm{LRMES}$ — An increase in the risk attributes of a firm, such as the correlation or volatility, also contributes to SRISK.

To view the changes in SRISK over a period of time in the Systemic Risk Analysis pages on V-Lab, click the 'View Changes' checkbox at the top of the SRISK table. A drop-down will appear which will allow you to select a time period and the SRISK table format will change to the SRISK Decomposition format, which will display the SRISK values for both time periods, $\Delta \mathrm{SRISK}$, $\Delta \left(\mathrm{DEBT}\right)$, $\Delta \left(\mathrm{EQUITY}\right)$, and $\Delta \left(\mathrm{RISK}\right)$.

Systemic Risk Capacity and Probability of Crisis

When financial firms are under-capitalized, they are vulnerable to external shocks. This is commonly measured by stress tests or market-based measures of systemic risk such as SRISK. The natural response to such vulnerability is to raise capital, and this can endogenously start a financial crisis. Excessive credit growth can be interpreted as under-capitalization of the financial sector. Hence, it is possible to assess how much SRISK an economy can stand, and measure the probability of a crisis.

In Ruan and Engle (2018), a Tobit model for 23 developed economies is estimated using a crisis severity variable constructed by Romer and Romer (2017). They develop a model of the impact of under-capitalization on the probability of crisis from the Tobit estimates. This model can be solved to obtain a corresponding SRISK capacity measure, which is defined as the level of SRISK that would keep the probability of crisis below 50%. These reveal the important global externalities since the risk of a crisis in one country is strongly influenced by the under-capitalization of the rest of the world.

On the welcome page for the Global SRISK Analysis (GMES), users can view plots of both the Probability of Crisis measure and SRISK Capacity measure from the global model developed by Ruan and Engle (2018). To view these, simply select select a single country from the drop down menu at the top of the page. SRISK Capacity for the selected country will be plotted alongside SRISK. Probability of Crisis will appear in a separate plot below the plot of SRISK and SRISK Capacity. These plots will only be visible when exactly one country has been selected, and when that country is among the 23 developed countries included in Romer and Romer (2017).

Fama, Eugene F. and Kenneth R. French, 1992. The cross-section of expected stock returns. Journal of Finance 47: 427-465. https://onlinelibrary.wiley.com/doi/full/10.1111/j.1540-6261.1992.tb04398.x

Acharya, Viral V., Christian T. Brownlees, Farhang Farazmand, and Matthew Richardson, 2011, "Measuring Systemic Risk," Regulating Wall Street: The Dodd-Frank Act and the New Architecture of Global Finance, chapter 4 (Wiley Publisher).

Acharya, Viral V., Robert F. Engle, and Matthew Richardson, 2012, Capital Shortfall: A New Approach to Ranking and Regulating Systemic Risks, American Economic Review: Papers and Proceedings 102, pp. 59–64

Brownlees, Christian T., and Robert F. Engle, 2017, SRISK: A Conditional Capital Shortfall Index for Systemic Risk Measurement, Review of Financial Studies.

Engle, Robert F., 2016, Dynamic Conditional Beta, Journal of Financial Econometrics 14, 643–667.

Engle, Robert F. and Tianyue Ruan, 2018, "How Much SRISK Is Too Much?", Available at SSRN: https://ssrn.com/abstract=3108269 or http://dx.doi.org/10.2139/ssrn.3108269

Romer, Christina D, and David H Romer, 2017, "New Evidence on the Impact of Financial Crises in Advanced Countries", American Economic Review107, 3072–3118.